Perceptrons in AI: The Building Blocks of Machine Learning

Last Edited

by

Miguel Vieira Pinto

in

,

Artificial Intelligence (AI) has rapidly evolved from the stuff of science fiction to a transformative reality that impacts virtually every industry today. From chatbots that offer customer service, to complex algorithms that predict weather patterns, the applications are as varied as they are impactful. Yet, to fully appreciate the strides AI has made, it’s crucial to understand its building blocks.

One such foundational element is the Perceptron—a simple yet powerful mathematical model that paved the way for neural networks and modern machine learning. In this comprehensive guide, we’ll delve deep into the world of Perceptrons, exploring their history, functionality, applications, and limitations. Whether you’re an AI novice or a seasoned professional, this article aims to enrich your understanding of this critical AI component.

In this article:

  1. What is a Perceptron?
  2. Historical Background
  3. How Does a Perceptron Work?
  4. Single-layer vs. Multi-layer Perceptrons
  5. Applications of Perceptrons
  6. Limitations of Perceptrons
  7. Conclusion
  8. More Resources
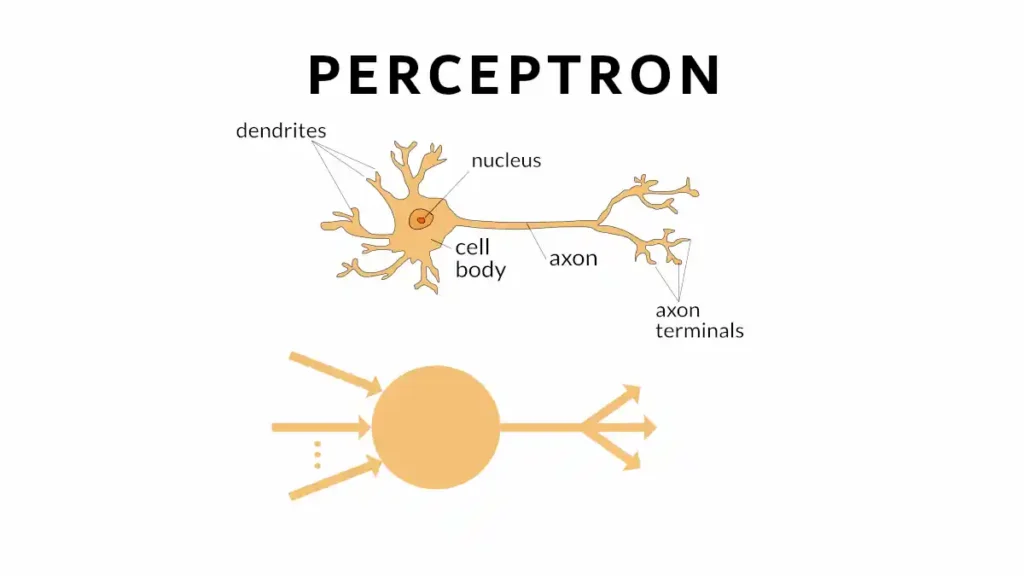
What is a Perceptron in AI?

1. What is a Perceptron?

A Perceptron is one of the simplest forms of artificial neural networks and serves as a fundamental building block for more complex neural architectures. Often described as a binary classifier, it essentially functions as a decision-making model, helping to sort input data into specific categories. The Perceptron is a mathematical model that mimics a biological neuron’s behavior to an extent, making it one of the earliest and most straightforward types of artificial neurons.

Core Components

  1. Input (X): The Perceptron receives a set of inputs, which are typically feature vectors from a dataset. These inputs can be numerical or categorical values, which are converted into a format that the Perceptron can understand.
  2. Weight (W): Each input is assigned a weight that represents its importance in the decision-making process. The weight is a real number that is adjusted during the learning phase.
  3. Bias (b): The bias allows the Perceptron to have some flexibility in its decision-making, essentially shifting the decision boundary away from the origin. Without a bias, the Perceptron would be constrained to make decisions based solely on its weighted inputs, which limits its capability.
  4. Activation Function (f): This function determines the output of the Perceptron. It takes the weighted sum of the inputs and bias and transforms it into an output value. Common activation functions include the step function, sigmoid function, and ReLU (Rectified Linear Unit).

Mathematical Representation

The output Y of a Perceptron is calculated using the following formula:

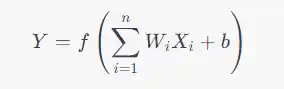
Perceptron mathematical representation: Y=f(i=1∑n​Wi​Xi​+b)

Here, f is the activation function, Wi​ represents the weight of the ith input Xi​, and b is the bias. The summation runs over all n inputs.

Basic Diagram

      [Input 1] ---> (* w1)
                        |
                        |
      [Input 2] ---> (* w2)   --->  [∑] ---> [Activation Function] ---> [Output]
                        |
                        |
      [Input n] ---> (* wn)
                        |
                        |
      [Bias]    ---> (+ b)

In this diagram:

  • Arrows represent the flow of data.
  • ∗wi​ represents the multiplication of each input by its respective weight.
  • ∑ signifies the summation of all weighted inputs plus the bias.
  • The Activation Function block shows the application of the activation function to the summed value to produce the output.
Back to Index

2. Historical Background

The journey of Perceptrons began in the late 1950s when American psychologist Frank Rosenblatt introduced the concept. Funded by the U.S. Office of Naval Research, Rosenblatt aimed to develop a machine that could mimic the human brain’s ability to recognize patterns and learn from experience. The Perceptron was groundbreaking at the time because it was among the first algorithms that could learn from its data—a revolutionary concept that had profound implications for the future of AI.

In essence, the Perceptron became the prototype for the artificial neurons used in today’s neural networks. Its invention sparked both enthusiasm and skepticism, giving rise to a broad field of research, encompassing machine learning, pattern recognition, and beyond. However, the initial hype surrounding Perceptrons was dampened by Marvin Minsky and Seymour Papert’s 1969 book “Perceptrons,” which pointed out some limitations of the model, particularly its inability to solve problems that aren’t linearly separable. This critique led researchers to explore more complex architectures, eventually leading to the development of multi-layer neural networks and other advanced algorithms that make up contemporary AI.

Back to Index

3. How Does a Perceptron Work?

Understanding the Perceptron’s operation may seem daunting, but breaking it down into a series of steps makes it easier to digest. Let’s dive into the fascinating mechanics of how a Perceptron works in a machine learning context.

Step-by-step Walkthrough

  1. Initialization:
    • When a Perceptron is first created, its weights and bias are initialized. These can be set to zero, random numbers, or based on some other criterion.
  2. Input Reception:
    • The Perceptron receives a set of inputs, often represented as a feature vector X=[X1​,X2​,…,Xn​].
  3. Weighted Summation:
    • Each input Xi​ is multiplied by its corresponding weight Wi​.
    • These weighted inputs are summed together, and the bias b is added to this sum.
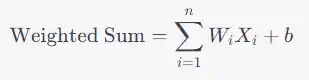
Weighted Summation: i=1∑n​Wi​Xi​+b
  1. Activation:
    • The weighted sum is passed through an activation function f to produce the output Y.

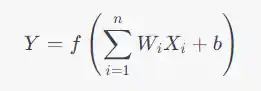
The weighted sum is passed through an activation function f to produce the output Y -> Y=f(i=1∑n​Wi​Xi​+b)
  1. Output Decision:
    • The value of Y is used to make a decision. In the case of a binary classifier, a common activation function like the step function might output either 0 or 1, representing two different classes.
  2. Learning and Adjustment:
    • After obtaining the output, the Perceptron compares it against the expected output or ground truth.
    • Based on the error, the weights and bias are adjusted to improve future predictions. This is typically done using learning algorithms like the Perceptron Learning Algorithm.

Simplified Math Explanation

  • Weighted Sum: Imagine you’re balancing a seesaw, and each input is a person with a weight that determines how much they tip the balance. The weighted sum is like finding the total influence of all these people on the seesaw, including a fixed ‘bias’ weight that you add to one side.
  • Activation Function: Think of this as a decision-making rule. For example, if the seesaw tips more to one side (weighted sum crosses a certain threshold), you decide to take action A (output 1); otherwise, you take action B (output 0).
  • Learning and Adjustment: If the seesaw isn’t balanced the way you want (output doesn’t match expected), you ask some people to change their positions (adjust weights) or add/subtract fixed weights (adjust bias) to tip the balance favorably next time.

By understanding these steps, you’re well on your way to grasping more complex neural network architectures that employ Perceptrons as their fundamental building blocks. The beauty of the Perceptron lies in its simplicity, which allows it to serve as an excellent introductory point for understanding the world of machine learning algorithms.

Back to Index

4. Single-layer vs. Multi-layer Perceptrons

When we talk about Perceptrons, it’s essential to distinguish between single-layer and multi-layer architectures. While both forms share the foundational principles, they differ significantly in complexity, capabilities, and applications.

Differences

  1. Complexity:
    • Single-layer Perceptrons are simpler and consist of just one layer of artificial neurons.
    • Multi-layer Perceptrons have one or more hidden layers in addition to the input and output layers, making them more complex.
  2. Problem Solving Capabilities:
    • Single-layer Perceptrons can only solve linearly separable problems, like the classic AND or OR logical operations.
    • Multi-layer Perceptrons can tackle non-linear problems, which widens their applicability considerably.
  3. Training Algorithms:
    • Single-layer Perceptrons typically use simple learning algorithms like the “Perceptron Learning Algorithm.”
    • Multi-layer Perceptrons often use backpropagation, a more sophisticated algorithm that adjusts weights and biases across multiple layers.
  4. Computational Overhead:
    • Single-layer Perceptrons are computationally cheaper but less powerful.
    • Multi-layer Perceptrons require more computational resources but are more capable.

Use Cases

  1. Single-layer Perceptrons:
    • Classification problems where data is linearly separable.
    • Basic pattern recognition.
  2. Multi-layer Perceptrons:
    • Complex classification and regression problems.
    • Speech and handwriting recognition.
    • Natural language processing.
Back to Index

5. Applications of Perceptrons

Perceptrons have seen a wide range of applications, both historically and in the contemporary tech landscape.

Historical Applications

  1. Character Recognition: One of the earliest applications, dating back to the 1960s, involved using Perceptrons for character and digit recognition. Although primitive by today’s standards, this was groundbreaking at the time.
  2. Basic Logical Operations: In educational settings and early research, Perceptrons were often used to demonstrate the learning of basic logical operations like AND, OR, and NOT.

Modern Applications

  1. Spam Filters: Single-layer Perceptrons can be quite effective in classifying emails as spam or not-spam based on keyword analysis.
  2. Quality Control: In manufacturing, Perceptrons can be used for simple quality checks, like determining if a product meets specific measurements.
  3. Text Classification: Multi-layer Perceptrons have been used in natural language processing tasks like sentiment analysis or categorizing documents.
  4. Computer Vision: Though more complex architectures are generally preferred for advanced vision tasks, Perceptrons still find use in basic image recognition activities.
  5. Medical Diagnosis: In healthcare, Perceptrons have been employed for basic diagnostic tasks like determining whether a tumor is malignant or benign based on a set of features.

By understanding where and how Perceptrons are applied, we can better appreciate their significance and versatility in the ever-expanding realm of AI and machine learning.

Back to Index

6. Limitations of Perceptrons

Despite their simplicity and ease of implementation, Perceptrons have several limitations that can be significant hurdles for certain types of problems.

What Perceptrons Can’t Do

  1. Non-Linear Problems: Single-layer Perceptrons can only solve linearly separable problems. This limitation means they can’t handle tasks like XOR logic gate implementation, which requires a non-linear decision boundary.
  2. Global Optimization: Perceptrons, especially in their simplest form, do not have mechanisms for global optimization. They can get stuck in local minima during the learning phase.
  3. Limited Complexity: Even multi-layer Perceptrons suffer from limitations in handling highly complex and nuanced tasks that require deep learning architectures.
  4. Inefficient for Large Networks: As the size of the network grows, the computation and resource requirements for training Perceptrons can become a bottleneck.

Development of Advanced Networks

These limitations led to the development of more complex neural network architectures like Convolutional Neural Networks (CNNs) for image processing, Recurrent Neural Networks (RNNs) for sequence data, and many others. Advanced optimization algorithms and training techniques were also developed to address these shortcomings, providing the foundation for modern AI as we know it today.

Back to Index

7. Conclusion

Perceptrons play an indispensable role in the foundation of Artificial Intelligence and machine learning. Serving as the building blocks for more complex neural networks, they have helped shape the field in its early years and continue to offer valuable insights into learning algorithms. While they have limitations in complexity and applicability, the principles they introduce are crucial stepping stones for anyone looking to understand AI deeply.

In this article, we’ve explored the core components, working mechanisms, types, applications, and limitations of Perceptrons. If this intrigues you, consider diving deeper into the fascinating world of AI, where a wealth of knowledge and practical applications await.

Back to Index

8. More Resources

  1. Books
  2. Papers
  3. Courses
  4. Online Blogs and Tutorials
Back to Index

Search