In the sprawling universe of artificial intelligence and machine learning, there exists a mathematical beacon that has been pivotal in elucidating intricate probabilistic interrelations. Known as Bayesian Networks, these structures interweave the foundational threads of statistics and graph theory to paint vivid pictures of intricate systems. As we stand on the cusp of a new AI-driven era, understanding these networks becomes paramount—not just for researchers and developers but for anyone intrigued by the machinations of intelligent systems.
In this article:
- What is a Bayesian Network?
- Historical Foundations
- Graph Theory & Probability
- Key Terminologies
- Building a Bayesian Network
- Real-world Applications
- Bayesian Networks vs. Neural Networks
- Further Reading
This article endeavors to decode the layered complexities of Bayesian Networks, translating rigorous mathematical formalisms into palatable insights. By the end, you’ll not only grasp the fundamental underpinnings but also appreciate the profound implications they hold for modern AI.
Unraveling the Enigma: What is a Bayesian Network?
At the crossroads of probability theory and graph theory lies the Bayesian Network. In essence, it’s a graphical model that represents the probabilistic relationships among a set of variables. The structure consists of nodes (representing variables) and directed edges (depicting conditional dependencies). The true power of a Bayesian Network is its ability to capture conditional independence between variables, facilitating efficient computation of joint probabilities, even in high-dimensional spaces.
» You may also like to read: The Turing Test!
Historical Foundations
Bayesian Networks, while appearing exceptionally avant-garde, have roots stretching back centuries, anchored deeply in the annals of statistical thought. Their genesis can be linked to the Reverend Thomas Bayes, an 18th-century statistician and theologian, whose work on probability theory laid the groundwork for what we now call Bayesian inference. Bayes’ revolutionary insight was to update probability estimates in light of new data—a principle encapsulated in Bayes’ theorem.

However, the explicit structure we recognize as Bayesian Networks emerged much later, in the mid-20th century. Key figures like Judea Pearl championed their development. Pearl, often dubbed the ‘father of Bayesian Networks,’ introduced the directed acyclic graph framework, giving a visual structure to intricate probabilistic interdependencies. The 1980s and 1990s witnessed an upsurge in interest, driven by the desire to develop more intuitive and computationally efficient frameworks for understanding complex systems in fields like AI and genetics.
Graph Theory & Probability
Bayesian Networks meld two dominant mathematical fields: graph theory and probability. At their core, these networks are directed acyclic graphs (DAGs), a fundamental concept in graph theory. In a DAG, nodes are connected by edges in a manner that avoids any closed loops. Each node in a Bayesian Network represents a random variable, while the edges signify probabilistic dependencies.
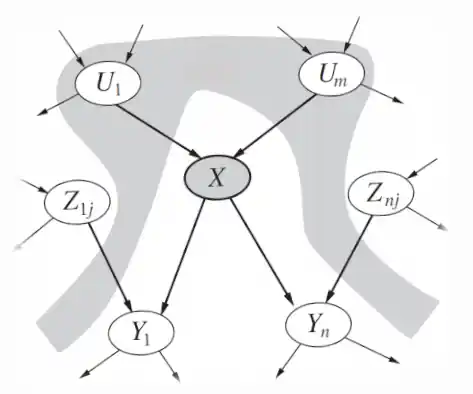
The probability aspect enters when we adorn these nodes and edges with quantitative information. Every node is associated with a probability function that takes, as input, a particular set of values for the node’s parent variables and gives the probability of the variable represented by the node. This probabilistic layering transforms the DAG into a rich, dynamic model, capable of representing intricate conditional dependencies and facilitating complex probabilistic queries.
» To read next: Machine Learning Basics
Key Terminologies
- Node: A distinct point in a network, representing a specific random variable.
- Edge: A line connecting two nodes, signifying a probabilistic dependency between the connected variables.
- Parents and Children: In the context of a Bayesian Network’s DAG structure, the nodes directing edges towards a particular node are its ‘parents’, while those receiving edges from it are its ‘children’.
- Conditional Independence: A property where two variables are independent when conditioned on a third variable. In Bayesian Networks, this is crucial in simplifying computations and understanding the structure of the network.
- D-separation: A criterion to determine whether a particular set of nodes in the graph blocks the flow of probabilistic information between two other non-adjacent nodes. Understanding d-separation is key to mastering the nuances of conditional independence in Bayesian Networks.
- Joint Probability Distribution: The probability distribution encompassing all the variables within a network. It is a foundational concept, as the entire Bayesian Network is effectively a compact representation of this distribution.
- Belief Propagation: An algorithm used in Bayesian Networks for the computation of posterior probabilities, allowing efficient inference in the network.
Through the amalgamation of these terminologies, one can begin to converse and conceptualize with fluency in the realm of Bayesian Networks, aiding in both comprehension and application.
Building a Bayesian Network
Building a Bayesian Network is a meticulous endeavor that melds domain knowledge with mathematical acumen. At its heart, it’s a dance between intuitive reasoning about the domain of interest and rigorous probabilistic formulation. Let’s delve into the intricate steps involved in crafting such a network:
1. Domain Understanding and Variable Identification
- Before one can draw a single node or edge, it’s essential to gain a thorough understanding of the problem domain.
- Enumerate all the variables (or factors) that play a pivotal role in the domain. Each of these will serve as nodes in your network.
2. Structuring the Network with Edges:
- Begin by visualizing the causal relationships between variables. For instance, in a medical diagnostic setting, a disease might cause several symptoms.
- Represent these causal relationships as directed edges between nodes. This is where domain expertise is paramount, ensuring that the connections mirror real-world interdependencies.
3. Parameterization via Conditional Probability Tables (CPTs):
- For every node, you’ll define a conditional probability table. If a node has no parents (it’s not influenced by any other nodes), this table simply describes the node’s marginal probability distribution.
- For nodes with parents, the CPT will list the conditional probabilities of the node taking on each of its possible values for every possible combination of its parents’ values.
- Acquiring accurate CPTs can be a challenge. Often, they’re populated using a blend of domain knowledge, empirical data, and sometimes, even educated guesses.
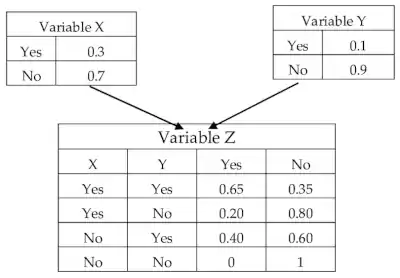
4. Incorporating Observational Data
- Bayesian Networks thrive on data. Observations, or data points, can be used to update the initial probabilities in the network using Bayesian inference.
- This is an iterative process—each new piece of data refines the network, enhancing its predictive prowess.
5. Validation and Testing of the Bayesian Network
- Once constructed, it’s crucial to validate the network. Does it behave as expected? Do its predictions align with empirical reality?
- Split your data (if you have a sizable dataset) into a training set and a test set. While the training set aids in fine-tuning the network’s probabilities, the test set assesses its predictive accuracy.
6. Iterative Refinement
Rarely is a Bayesian Network perfect in its first incarnation. Often, post-deployment observations will necessitate adjustments.
Whether it’s adding new nodes, altering conditional probabilities, or restructuring relationships, refinement is an ongoing process. It’s this adaptability, though, that grants Bayesian Networks their dynamism and robustness.
7. Inference and Utility
- With a well-calibrated network, one can now perform queries and draw probabilistic inferences. Whether it’s determining the likelihood of an outcome given certain evidence or assessing scenarios under uncertainty, the Bayesian Network serves as a potent analytical tool.
8. Expansion and Scalability:
- As with all models, change is inevitable. Over time, one might find the need to integrate more variables or new relationships. The structure of Bayesian Networks lends itself well to such expansions. Yet, it’s important to note that as networks grow, the complexity of computations can escalate, demanding more sophisticated algorithms or computational resources.
Constructing a Bayesian Network, while undoubtedly intricate, is a deeply rewarding exercise. It distills nebulous uncertainties into a structured graphical form, offering a potent lens to gaze upon complex probabilistic landscapes.
» You should also read: What are Transformers in AI?
Real-world Applications
Bayesian Networks have etched a mark that’s both indelible and awe-inspiring. Their capacity to grapple with uncertainty, marrying domain knowledge with empirical data, has engendered a slew of applications across multifarious domains.
Let’s embark on a riveting journey across the terrains where these networks have showcased their mettle:
Medical Diagnosis
The medical realm, rife with complexities and uncertainties, is a fertile ground for Bayesian Networks. Physicians harness their prowess to discern potential diseases given a set of symptoms, offering a probabilistic viewpoint that traditional deterministic models might eschew.
Beyond just diagnosis, these networks aid in treatment recommendation, mapping a patient’s response to various therapeutic interventions based on their medical history and genetic predispositions.
Robotics and Automation
Navigating the real world, with its unpredictable vicissitudes, demands robots to be adept at probabilistic reasoning. Bayesian Networks empower these mechanical marvels to make sense of sensor data, decode environmental cues, and chart out actions that hedge against uncertainty.
Financial Forecasting
The volatile dance of stock markets, with its cascading ramifications, finds a reliable partner in Bayesian Networks. Financial analysts leverage these networks to predict market movements, taking into account a medley of variables—from geopolitical events to corporate earnings.
Natural Disaster Prediction
Predicting Mother Nature’s caprices—be it hurricanes, tsunamis, or earthquakes—is an endeavor where Bayesian Networks have exhibited promise. By integrating data from diverse sources and parsing historical patterns, they proffer probabilistic insights that can galvanize preemptive actions.
Criminal Forensics and Investigation
In the intricate puzzle of crime-solving, Bayesian Networks emerge as invaluable assets. They assist investigators in weighing evidence, considering alternative hypotheses, and estimating the likelihood of various scenarios, thereby streamlining the path to truth.
Genetics and Bioinformatics
The biological cosmos, with its entangled webs of gene interactions, finds a semblance of order with Bayesian Networks. Researchers deploy them to elucidate gene regulatory networks, predict phenotypic outcomes, and even delve into evolutionary trajectories.
The forays of Bayesian Networks into these domains underscore their versatility and attest to their transformative potential. It’s a testament to how an abstract mathematical framework can translate into tangible real-world impact.
Bayesian Networks vs. Neural Networks
In the resplendent pantheon of artificial intelligence, where myriad architectures jostle for prominence, Bayesian Networks and Neural Networks emerge as two luminaries, each illuminating distinct facets of computational reasoning. To the uninitiated, they might seem akin, but beneath the surface, they harbor profound distinctions. Let’s traverse this fascinating dichotomy:
Philosophical Underpinnings
Bayesian Networks find their roots in probabilistic graphical models, where the emphasis is on explicating relationships between variables and reasoning under uncertainty. They offer a transparent, structured view of the problem space.
Neural Networks, conversely, are inspired by biological neural systems. Their modus operandi involves learning patterns from data, often eschewing explicit modeling of relationships.
Transparency and Interpretability
The structured nature of Bayesian Networks renders them highly interpretable. Each node, edge, and probability value tells a coherent story, allowing for easy insights into the modeled relationships.
Neural Networks, often dubbed as “black boxes,” might excel in pattern recognition but often do so at the cost of transparency. Their deeply layered architectures can obfuscate the exact rationale behind decisions.
Training and Learning
Bayesian Networks thrive on domain expertise and observational data, leveraging Bayesian inference to update probabilities. Their learning is often an amalgamation of prior beliefs and empirical evidence.
Neural Networks lean heavily on data, relying on gradient-based optimization techniques to tweak their millions of parameters. They’re quintessentially data-driven, often demanding sizable datasets for effective training.
Flexibility and Adaptability:
Bayesian Networks are inherently flexible, accommodating new variables, and relationships with relative ease. Their probabilistic foundation allows them to gracefully handle missing data and make predictions under varying degrees of certainty.
Neural Networks, while powerful, can be more rigid. Introducing new data or making structural changes often necessitates retraining from scratch.
Computational Overheads:
For large, intricate Bayesian Networks, inference can be computationally intensive, especially when dealing with a plethora of interconnected variables.
Neural Networks, particularly deep learning variants, are notorious for their voracious appetite for computational resources during training phases. However, once trained, they can make predictions at lightning speeds.
While both architectures have carved their niches and celebrated successes, their choice is often governed by the problem’s nature, available data, and the desired trade-off between interpretability and predictive prowess. In the ever-evolving AI landscape, they stand as complementary tools, each with its unique allure and applicability.
Further Reading
Diving deep into Bayesian Networks requires reliable resources that cater to both neophytes and seasoned aficionados. Here’s a curated list of books, papers, and websites that illuminate the Bayesian landscape:
Books:
- “Probabilistic Graphical Models: Principles and Techniques” by Daphne Koller and Nir Friedman: A magnum opus that delves deep into the world of Bayesian Networks and Markov Fields.
- “Bayesian Networks and Decision Graphs” by Finn V. Jensen: A lucid introduction to the foundations and applications of Bayesian Networks.
- “Bayesian Artificial Intelligence” by Kevin B. Korb and Ann E. Nicholson: A comprehensive exploration of Bayesian Networks in the realm of AI, encompassing theory and practice.
Papers:
- “A Bayesian Hierarchical Model for Learning Natural Scene Categories“: A seminal paper that investigates the use of Bayesian Networks in computer vision.
- “Learning Bayesian Networks: The Combination of Knowledge and Statistical Data“: A deep dive into the fusion of domain expertise and empirical data in the training of Bayesian Networks.
Websites:
- BayesiaLab: A platform replete with tools, webinars, and tutorials catered to Bayesian Network enthusiasts.
- bnlearn: An R package for Bayesian Network learning and parameter estimation. The website provides tutorials, case studies, and resources to navigate this package.
Courses:
- Coursera’s “Probabilistic Graphical Models Specialization”: A series of courses that unravel the mysteries of Bayesian Networks and their kin, taught by the luminary, Prof. Daphne Koller.
As with any topic, immersing oneself in Bayesian Networks demands dedication and an insatiable curiosity. But, equipped with the right resources, the journey is both enlightening and profoundly rewarding.