Definition of AGENT in Network Encyclopedia.
What is Agent SNMP
Agent in SNMP is a Simple Network Management Protocol client software that runs on a hub, a router, or another networking component. Agents collect information about TCP/IP statistics and conditions and can supply this information when requested to an SNMP management system. Agents can also alert management systems to errors and other conditions when a trap occurs. SNMP agents are identified by the community to which they belong.
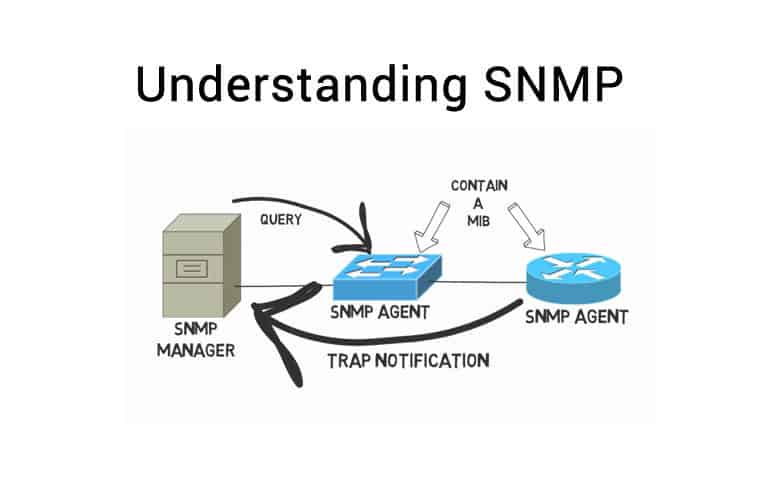
How Agent works
An agent must be installed on each networking component that will be managed in an SNMP-managed network. The agent program can then perform operations such as
- Get operations initiated by the SNMP management console for obtaining information about a specific managed object in the host Management Information Base (MIB)
- Get-next operations initiated by the management console to continue traversing the MIB database from the point at which it was accessed by a get operation
- Set operations initiated by the management console to set a value for a managed object (if permissions allow this)
- Trap operations initiated by the managed host itself when an error condition occurs, such as when the computer’s disk becomes full
Microsoft Windows NT includes an optional service called the SNMP service, which can be used to install SNMP agent software to enable management by SNMP management consoles. TCP/IP must be installed before the SNMP agent service is installed. By default, the agent listens to TCP port number 161 for SNMP messages and to port number 162 for SNMP traps.
TIP: Windows 98 also includes an SNMP agent conforming to SNMP 1.0 specifications that lets you monitor remote connections to machines running Windows 98 from an SNMP management console. This agent is implemented as a Win32 service using Windows Sockets over TCP/IP. You can install the Microsoft SNMP agent on Windows 98 using the Network utility in Control Panel. SNMP Agents are identified with the community to which they belong.