Basics of Satellite Communication. How it works. Digital Communication by Satellite.
What is Satellite Communications?
Satellite communications is an extension of LOS microwave technology. The satellite must be within line-of-sight of each participating earth terminal. We are more concerned about noise in satellite communication links than we were with LOS microwave. In most cases, received signals will be of a much lower level.

On satellite systems operating below 10 GHz, very little link margin is required; there is no fading, as experienced with LOS microwave. The discussion here only deals with geostationary orbit (GEO) communication satellites.
Satellite communications present another method of extending the digital network. These digital trunks may be used as any other digital trunks for telephony, data, the Internet, facsimile, and video. However, fiber optics has become a strong competitor of satellite communications. Only very small aperture terminal (VSAT) systems are showing any real growth in the GEO arena. A new type of communication satellite is being fielded.
Sponsored link: Winegard GM-6035 Carryout G2+ Automatic Portable Satellite TV Antenna with Power Inserter (RV Satellite for DIRECTV, DISH, BellTV) – Black
Satellite Communications basics
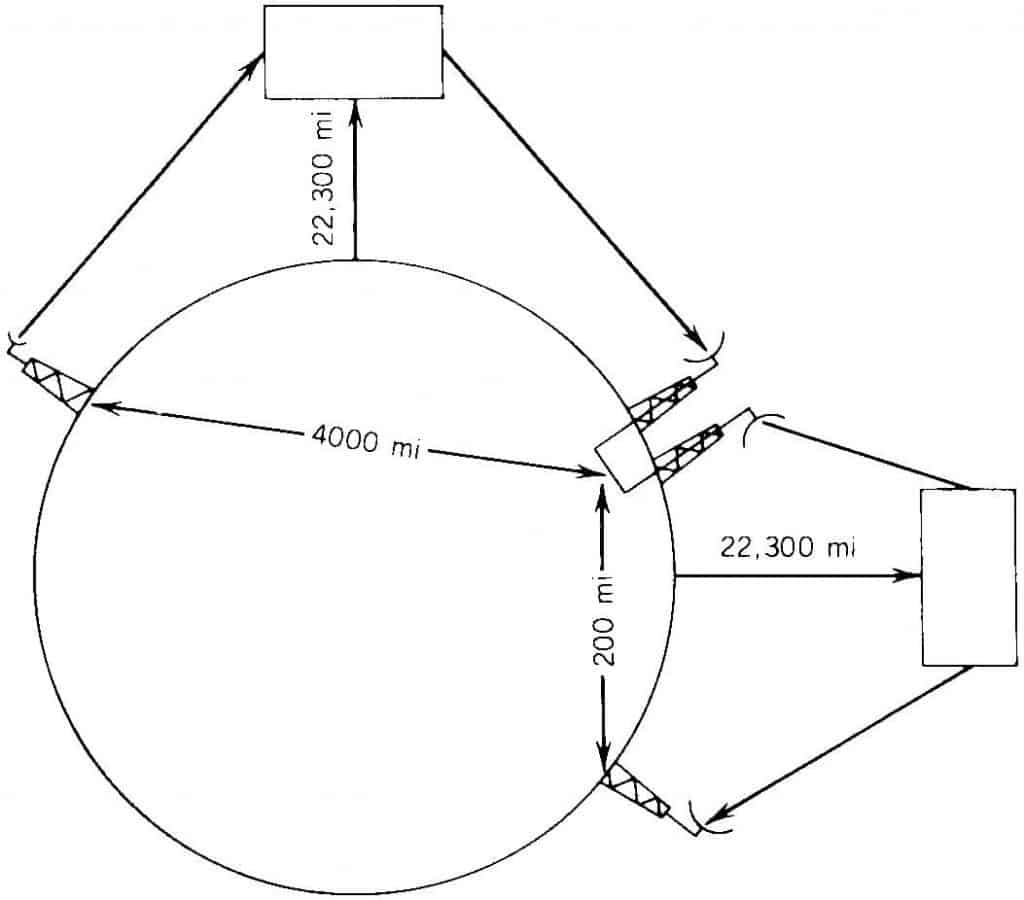
Satellite communication is nothing more than LOS microwave using one (or two) satellites located at great distances from the terminal earth stations, as illustrated in Figure 2 Because of the distance involved, consider the slant range from the earth station to the satellite to be the same as the satellite altitude above the equator. This would be true if the antenna were pointing at zenith (08 elevation angle) to the satellite. Distance increases as the pointing angle to the satellite decreases (elevation angle).
We thus are dealing with very long distances. The time required to traverse these distances – namely, earth station to satellite to another earth station – is on the order of 250ms. Round-trip delay will be 2 × 250 or 500 ms. These propagation times are much greater than those encountered in conventional terrestrial systems. So one major problem is propagation time and resulting echo on telephone circuits. It influences certain data circuits in a delay to reply for block or packet transmission systems and requires careful selection of telephone signaling systems, or call-setup time may become excessive.
Naturally, there are far greater losses. For LOS microwave we encounter free-space losses possibly as high as 145 dB. In the case of a satellite with a range of 22,300mi operating on 4.2 GHz, the free-space loss is 196 dB and at 6 GHz, 199 dB. At 14GHz the loss is about 207 dB. This presents no insurmountable problem from earth to satellite, where comparatively high-power transmitters and very-high-gain antennas may be used. On the contrary, from satellite to earth the link is power-limited for two reasons: (1) in bands shared with terrestrial services such as the popular 4-GHz band to ensure noninterference with those services, and (2) in the satellite itself, which can derive power only from solar cells. It takes a great number of solar cells to produce the RF power necessary; thus the downlink, from satellite to earth, is critical, and received signal levels will be much lower than on comparative radio links, as low as −150 dBW.
A third problem is crowding. The equatorial orbit is filling with geostationary satellites. Radio-frequency interference from one satellite system to another is increasing. This is particularly true for systems employing smaller antennas at earth stations with their inherent wider beamwidths. It all boils down to a frequent congestion of emitters.
Frequency Bands: the most desirable
The most desirable frequency bands for commercial satellite communication are in the spectrum 1000–10,000 MHz.These bands are:
- 3700–4200 MHz (satellite-to-earth or downlink);
- 5925–6425 MHz (earth-to-satellite or uplink);
- 7250–7750 MHz (downlink);
- 7900–8400 MHz (uplink).
These bands are preferred by design engineers for the following primary reasons:
- Less atmospheric absorption than higher frequencies;
- Rainfall loss not a concern;
- Less noise, both galactic and man-made;
- Well-developed technology;
- Less free-space loss compared with the higher frequencies.
Multiple Access to a Communication Satellite
Multiple access is defined as the ability of a number of earth stations to interconnect their respective communication links through a common satellite. Satellite access is classified (1) by assignment, whether quasi-permanent or temporary, namely, (a) preassigned multiple access or (b) demand-assigned multiple access (DAMA); and (2) according to whether the assignment is in the frequency domain or the time domain, namely, (a) frequency-division multiple access (FDMA) or (b) time-division multiple access (TDMA). On comparatively heavy routes (≥10 erlangs), preassigned multiple access may become economical. Other factors, of course, must be considered, such as whether the earth station is “INTELSAT” standard as well as the space-segment charge that is levied for use of the satellite. In telephone terminology, “preassigned” means dedicated circuits. DAMA is useful for low-traffic multipoint routes where it becomes interesting from an economic standpoint. Also, an earth station may resort to DAMAas a remedy to overflow for its FDMA circuits.
There are three methods to handle digital communication by satellite: (1) TDMA, (2) FDMA, and (3) over a VSAT network. Digital access by FDMA is handled in a similar fashion as with an analog FDM/ FM configuration. Several users may share a common transponder and the same backoff rules hold; in fact they are even more important when using a digital format because the IM products generated in the satellite TWT high-power amplifier (HPA) can notably degrade error performance. In the link budget, once we calculate C/N0, we convert to Eb/N0 with the following formula:
Eb/N0 = C/N0 – 10 log(bitrate).The Eb/N0 value can now be applied to the typical curves found in Figure 9.10 to derive the BER.
As mentioned previously, satellite communication is downlink limited because downlinkEIRP is strictly restricted. Still, we want to receive sufficient power to meet error performance objectives. One way to achieve this goal is to use forward error correction on the links where the lower Eb/N0 ratios will still meet error objectives. Thus INTELSAT requires coding on their digital accesses.
The occupied satellite bandwidth unit for IDR carriers is approximately equal to 0.6 times the transmission rate. The transmission rate is defined as the coded symbol rate. To provide guard bands between adjacent carriers on the same transponder, the nominal satellite bandwidth unit is 0.7 times the transmission rate.