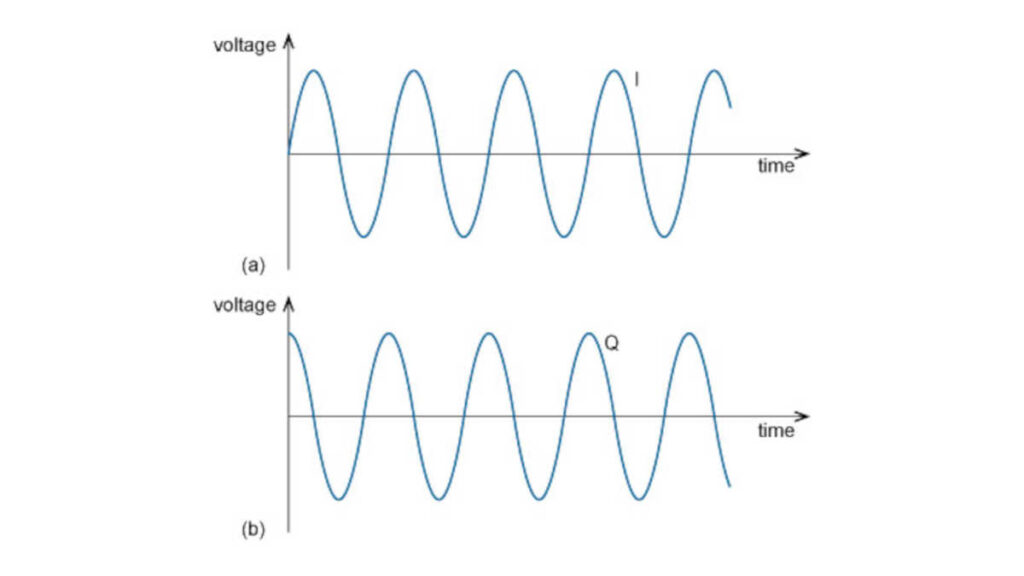
Quadrature amplitude modulation (QAM) is a method of encoding digital data on an analog carrier signal, such as a radio frequency (RF) or an optical carrier. In QAM, the digital data is modulated onto the carrier signal by varying the amplitude (i.e. the strength or power) of two carrier signals that are 90 degrees out of phase. These two carrier signals are known as the in-phase (I) and quadrature (Q) components of the QAM signal.
QAM is commonly used in telecommunications systems, such as cable television networks, digital subscriber line (DSL) networks, and wireless networks. It is also used in other applications where digital data needs to be transmitted over an analog medium, such as in satellite communication systems and in some forms of data storage.
One advantage of QAM is that it allows for a higher data rate than other analog modulation methods, such as frequency-shift keying (FSK) or phase-shift keying (PSK) because it encodes multiple bits of data onto each symbol (i.e. the combination of the I and Q signals). This makes QAM a popular choice for transmitting high-bandwidth data, such as video and audio.
Demodulation of Quadrature Amplitude Modulation
In a Quadrature Amplitude Modulation signal, one carrier lags the other by 90°, and its amplitude modulation is often called the in-phase component, denoted by I(t). The other modulating function is the quadrature component, Q(t). So, the composite waveform is mathematically modeled as:
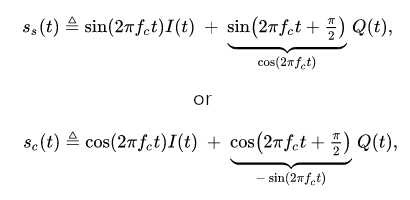
where fc is the carrier frequency. At the receiver, a coherent demodulator multiplies the received signal separately with both a cosine and sine signal to produce the received estimates of I(t) and Q(t).
Adding two sinusoids is a linear operation that creates no new frequency components. So, the bandwidth of the composite signal is comparable to the bandwidth of the DSB (Double-Sideband) components. Effectively, the spectral redundancy of DSB enables a doubling of the information capacity using this technique. This comes at the expense of demodulation complexity. synchronization is typically achieved by transmitting a burst subcarrier or a pilot signal. The phase reference for NTSC, for example, is included within its color burst signal.