Asymmetric encryption requires the use of two keys: a private key that is known only by its owner and a public key that is readily available to those who need to use it. It is important to note that asymmetric encryption has the property that figuring out one key from the other should be as hard as decrypting the message without any key.
Stated another way, the computational power required to decrypt an asymmetrically encrypted message is approximately the same as deducing one asymmetric key from the other.

In this article, we’ll look at how asymmetric encryption can be used for ensuring confidentiality and authentication.
Ensuring Confidentiality with Asymmetric Encryption
One of the primary uses of asymmetric encryption is to encrypt a symmetric encryption key. Alice creates the two keys required for asymmetric encryption and publishes one of them to the world.
Now everyone in the world, including Bob, has access to this key (Alice’s public key). This means Bob, or anyone else in the world, can encrypt data and send it to Alice for only Alice to read. Remember, the only person that can decrypt the cipher text is Alice or the person with Alice’s private key.
Now the problem of sharing a symmetric key is easy.
- Bob creates a symmetric key.
- He uses Alice’s public key to encrypt the symmetric key so no one else can read it.
- He sends the encrypted symmetric key to Alice.
- Alice receives the encrypted symmetric key, decrypts it with her private key, and begins communicating with Bob using the symmetric key he created.
But why would you use the symmetric key encryption algorithms at all? If asymmetric algorithms are secure and you already have everyone’s public key, why bother with creating a symmetric key and using symmetric algorithms?
The answer to that question is simple – for speed. Using RSA (a standard asymmetric encryption algorithm developed by Ron Rivest, Adi Shamir, and Len Adleman), assume that your computer can encrypt 35,633 1024-bit messages in 10 seconds.
Using AES, the standard for symmetric encryption in CBC mode, on the same computer you can encrypt 69,893 1024-bit messages in only 3 seconds. Using symmetric encryption is more than 6.5 times faster than using asymmetric encryption.
Assuming both algorithms are secure, why would you use one that is 6.5 times slower than the other?
Asymmetric encryption is slow because it uses properties of number theory to derive its strength. The addition and multiplication of these very large (1024-bit) numbers takes a very long time on computers compared to the binary operations performed in symmetric key encryption.
Even though asymmetric encryption is very slow, it does a very good job of solving the problem of sharing keys. Most symmetric algorithms have a key size somewhere around 128 to 256 bits. These keys can be encrypted in a single asymmetric message block, for most algorithms. This means only one message (the encrypted symmetric key) needs to be sent from Alice to Bob using an asymmetric algorithm before they can communicate using a symmetric algorithm.
Digital Signatures
A digital signature encrypts a message with a private key so that anyone can read it, but verify that it came from the holder of the private key because only the person who holds the private key can create cipher text that can be decrypted using the public key.
Using asymmetric encryption is really, really slow. Does this mean digital signatures are really slow as well? If the digital signature implementation encrypted the entire file, it would be slow. To alleviate this problem, the message is represented as a smaller message which is signed by Alice and sent along with the unencrypted original message.
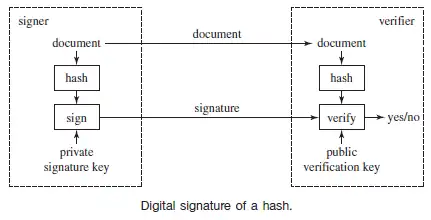
This smaller message is so small that it takes only a tiny amount of time to sign. Now anyone can read Alice’s message and can also verify that it truly came from her and no one else. You go about making this smaller message that represents the larger one with a hash function. We’ll discuss hash functions in another article.
References and Credits
- Wiley Pathways Network Security Fundamentals Project Manual, by Eric Cole, Ronald L. Krutz, James Conley, Brian Reisman, Mitch Ruebush, Dieter Gollman and Rachelle Reese.