Symmetric encryption, or single-key encryption, is the most well-understood cryptography primitive. It is where the whole field really started. Caesar and his cipher, the Germans and Enigma, and the Japanese and Purple are all examples of symmetric encryption. The idea behind symmetric encryption is that only a single key is used to both encrypt and decrypt a message.
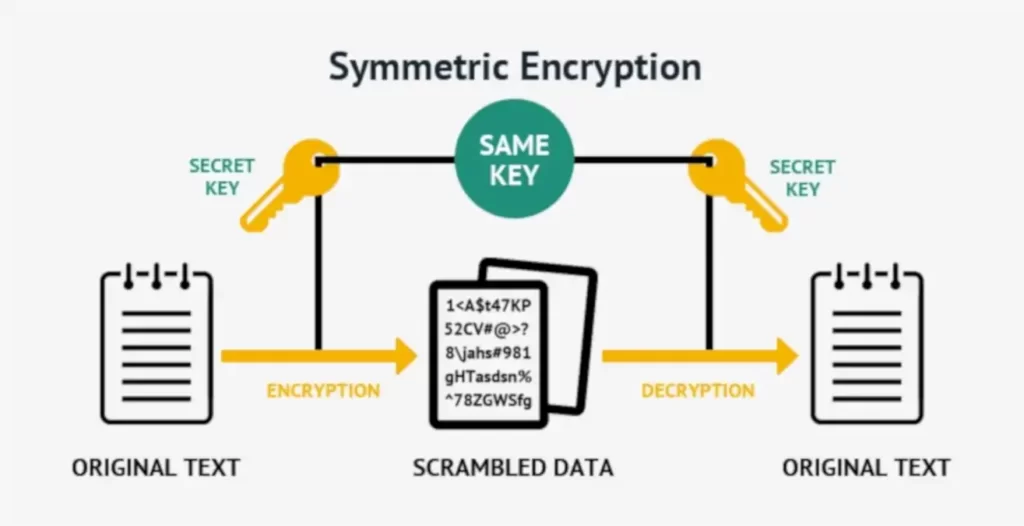
The benefit of using symmetric encryption is that it’s very fast. In this article, we’ll look at how symmetric encryption works, the types of ciphers used by different algorithms, and the main drawback to using symmetric encryption: exchanging keys.
In this article:
- Understanding Symmetric Encryption
- Encryption Strength
- Stream Ciphers
- Block Ciphers
- Sharing Keys
- References and Credits
If you’re looking for Asymmetric Encryption read this article.
Understanding Symmetric Encryption
Symmetric encryption is used when Alice wants to provide the confidentiality of a message she sends to Bob. Depending upon the mode of encryption used (modes are explained later in this article), symmetric encryption can also provide integrity when used correctly.
The best analogy for symmetric encryption is a lockbox. To unlock a lockbox you must have the right key. In the physical world, this key is usually a metal object. In the world of cryptography, this key is a set of random bits.
Whatever is inside the lockbox is confidential and protected from anyone without the key. Without the key, Mallory is unable to read, modify, or do anything to the data except destroy it (by destroying the lockbox). The same key is used to decrypt the data as is used to encrypt the data.
Encryption Strength
In our lockbox example, Mallory can attempt to open the safe by going through all possible physical configurations for a key until the proper configuration is tried and the safe is opened. In cryptography the same is true. Mallory can try all possible key combinations until one works, and the resulting data or message is understandable. You might be asking yourself, how many combinations would an attacker have to try? The answer to that question depends upon the encryption algorithm or cipher used. An algorithm is considered computationally secure if the amount of time needed to compute all possible combinations is so large that it cannot be done in any reasonable amount of time. This definition, “in a reasonable amount of time,” is deliberately vague, because the meaning of computationally secure is ever-changing as the speed of a computer is ever-increasing.
Also, most data does not need to be protected forever. Different types of data have different periods of time during which disclosure is a risk. After that time has elapsed, the data no longer needs to be kept confidential.
One popular symmetric encryption algorithm, Data Encryption Standard (DES), has a key of 56 bits. This means that breaking the algorithm would require 72,057,594,037,927,936 different keys to be tested to exhaust all possibilities.
Assuming a computer could try a million keys a second, it would take 2284 years to try all of the keys. That sounds like it is a secure algorithm because we will all be dead by the time the key is discovered. However, a specially built machine was used to crack DES in less than 56 hours.

Stream Ciphers
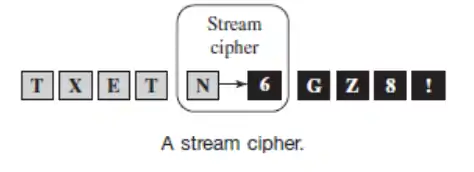
A stream cipher uses a single key to encrypt a message or stream of data. The message is considered to be a stream of data in that each byte is processed with the bytes preceding it, and the order is important. If you were to change the order of any of the bytes in the plain text, the cipher text, from that point forward, would look different. The figure below shows what a stream cipher does.
Stream ciphers normally do not require any padding of the message. Padding is adding extra bits to the message. Because messages are treated as a stream of data they can be of any length and do not need to be padded in any way except to add randomness to common messages.
You have already learned about one type of stream cipher, the one-time pad.
Other stream ciphers include the following:
▲ RC4
▲ SEAL (Software-Optimized Encryption Algorithm)
▲ ISAAC (stands for indirection, shift, accumulate, add, and count)
▲ Panama
▲ A5/1
▲ A5/2
▲ FISH (Fibonacci SHrinking)
▲ Helix
When Alice wants to send a message to Bob using a stream cipher, they must both have the same key and Bob must feed the cipher text into the algorithm in the same order as Alice fed the plain text into the algorithm to encrypt it.
Mallory can prevent Bob from decrypting most stream-cipher-encrypted messages by changing the first few bits that Alice sends to Bob. This property of a stream cipher is not always a bad thing. It provides integrity. If any of the cipher text bits are changed, it will be obvious to Bob when he decrypts the message.
There are some stream ciphers that do not propagate errors through the entire message. What this means is that if an error occurs while the message is being sent from Alice to Bob, it will only prevent that section of the message from being decrypted properly. This property is an important one to consider if the message will be sent across an unreliable connection.
Block Ciphers
A block cipher is the other kind of symmetric encryption algorithm. Block ciphers also use a single key to encrypt a message, but it is done one block at a time. A block is considered a certain number of bits and is determined by the algorithm. Each block is processed independently, and there is no correlation between the encrypting of one message block and another. The following figure shows what a block cipher does.
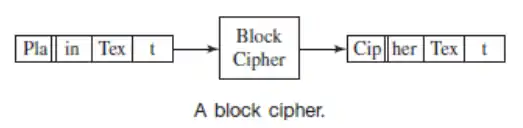
Because block ciphers have the ability to process a single block of the message independently, they need to include safeguards to prevent someone from gaining information about the message by seeing repeated blocks. For example, if Alice sends the message “yes” to Bob in response to a series of questions, the word “yes” will be encrypted to the same cipher text, assuming the same key is used. Then every time the word “yes” was sent, Eve would know what message was being sent without needing to decrypt it. Worse yet, Mallory could precompute the message “yes” with all possible keys and then simply match the cipher text seen to the cipher text of a pre-computed message. Assuming the key size was small enough, Mallory would be able to compute the corresponding key and break all further encryptions.
Another attack that Mallory can use is to change the order of blocks. This will not prevent decryption from occurring, as would happen with a stream cipher because no block depends on any other block. For example, suppose Alice asks Bob what his house number is and his response is “1234,” encrypting “12” in one block and “34” in another. Without knowing what house number was actually sent, Mallory can still change the ordering of the blocks and send Alice “3412,” the wrong house number. So, Mallory can change the ordering of the blocks without Bob or Alice knowing. Although the encryption method provides confidentiality, integrity can be broken.
To prevent the same plain text block from always encrypting to the same cipher text block, block ciphers use different encryption modes. The encryption modes are described as follows:
▲ Electronic code book (ECB): The message is encrypted one block at a time so that one plain text block maps to one cipher text block. An error in any block only affects the decryption of that block. If an entire block is lost during transmission, none of the other blocks are affected.
▲ Cipher-block chaining (CBC): The output block of the previous encryption is XORed with the next block of plain text before being encrypted. If a bit is changed in the plain text of one block, that change is propagated to all subsequent cipher text blocks. If a cipher text bit is changed, the current block will be corrupted and the changed bit will be inverted in the next block. CBC does not allow blocks to be encrypted in parallel. However, they can be decrypted in parallel.
▲ Propagating cipher-block chaining (PCBC): Similar to CBC, except that changes to the cipher text are propagated throughout the message. PCBC is the mode of operation used in Kerberos (an authentication protocol).
▲ Cipher Feedback (CFB): The previous cipher text block is XORed with the current encrypted text block. This differs from CBC mode in that the XOR occurs after the encryption of the current text block. If a bit in the cipher text is changed, the current block will have that bit inverted and the subsequent block will be corrupted.
▲ Output feedback (OFB): The output of the encryption algorithm is continually fed into the algorithm while the plain text is XORed with this output. This differs from CFB because what is fed into the encryption algorithm does not include the cipher text. If an error occurs in one block, that error is only propagated to those bits that are changed. However, if any of the bits are lost, including a whole block, the error is propagated to all of the remaining blocks and cannot recover.
ECB is almost never used because of the reasons stated. The most popular mode is CBC because errors do not propagate throughout the entire message if bits are lost like they do in OFB. CBC is used over CFB because the error propagation is usually smaller, only two blocks and because the bit changes that do occur happen in a predictable manner to the later blocks. For example, when using CBC, if Block 1 has bits flipped in it during transmission, Block 1 will be seemingly random, and Block 2 will have the exact bits flipped where they were in Block 1 during transmission.
This enables Mallory to cause predictable changes to the message. In CFB mode, bits flipped in Block 1 are the exact bits that are flipped in Block 1 of the deciphered message. The later blocks then appear random. If an attacker is going to flip bits while the cipher text is being transmitted, it is always better to receive a random-looking block on decryption, alerting you that tampering has occurred and to not trust anything that comes after the altered block. This is not true for CFB, because you cannot necessarily tell where the error begins—only that one has occurred.
DES (discussed previously) is only one of many block ciphers. DES was the original block cipher backed by a National Institute of Standards and Technology (NIST) publication. NIST is a United States government agency that performs research, develops technical standards, and promotes technological advances. However, because of the small key size involved in DES, 56 bits, it was only thought to be secure for 5 years because computers today can quickly perform a brute force attack against 56 bits. Triple DES (3DES) applies the DES algorithm to the plain text three times, for a key length of 168 bits. The primary drawback to 3DES is performance.
In 2001, NIST announced a new algorithm called Advanced Encryption Standard (AES), which was adopted as a standard in May 2002. AES has three key sizes: 128, 192, or 256 bits. The block size is 128 bits. AES has been approved by the National Security Agency (NSA), a United States government agency responsible for collecting and analyzing foreign communications and protecting the confidentiality of U.S. government data. AES has gained in popularity and is now a commonly used symmetric encryption protocol. A similar encryption algorithm, Rijndael, supports key and block sizes in any multiple of 32 between 128 and 256 bits.
Other block ciphers include, but are not limited to, the following:
▲ Desx
▲ Blowfish
▲ Cast
▲ Skipjack
▲ Twofish
There are many, many more.
Sharing Keys
With strong block ciphers created, the ability to use them is still hindered by the fact that the key must be known by both parties before the algorithm can be used. Often, the other party you are going to communicate with is known, so keys can be created and shared in a secure manner before communication begins.
This type of key generation is called using a pre-shared secret. The key is shared between parties before communication begins. However, what if Alice wants to communicate with Bob, but she has never met Bob before so that they do not have a pre-shared secret key? How then can Alice and Bob communicate securely? They could create keys and encrypt them so no one knows the keys, but how are they going to encrypt them without common keys?
One way to solve this problem is to use a trusted third party, Trent. Alice will create a key to be used to communicate with Bob. She will encrypt this key using a pre-shared key that she has with Trent and then send the key to Trent.
Trent will then be able to decrypt the key he received from Alice using their preshared key and then encrypt it with a key he has pre-shared with Bob and send it to him. Now both Alice and Bob have a common shared key, and only Trent, Alice, and Bob know what the key is. However, this scheme has problems, starting with Trent. What if Trent is really not Trent at all but Mallory? Now she has the key and can decrypt any communication between the two parties. Also, this scheme requires that the sending and receiving parties have a pre-shared key with Trent. Implementing a system like this would be a huge logistical problem.
Another way to share a key between two parties is for the parties to create the key on the fly, in a secure manner. A method for generating keys in this manner is called a key agreement protocol. One classic key agreement protocol is Diffie-Hellman key exchange.
For this protocol to work, both Alice and Bob agree to use a specific prime number (p) and a base number (g). Next, Alice and Bob each choose a secret integer. We’ll refer to Alice’s secret integer as “a” and Bob’s secret integer as “b”. Alice sends Bob the value of the following calculation:
ga mod p
Bob sends Alice the value of the following calculation:
gb mod p
Alice calculates the key by using the following formula:
Key = (Messagebob)a mod p
Bob calculates the key by using the following formula:
Key = (Messagealice)b mod p
Alice and Bob both calculate the same value for the key. However, Eve would need to determine both secrets a and b to arrive at the correct value. This is very difficult to do because it would require Eve to solve the discrete logarithm problem, for which efficient algorithms do not exist at this time.
However, a man-in-the-middle attack can be launched against this type of key agreement protocol, as shown in the figure below. In a man-in-the-middle attack, Mallory intercepts the message sent from Alice to Bob and that sent from Bob to Alice. She pretends to be Bob when Alice sends a message to Bob, and pretends to be Alice when Bob sends a message to Alice. With Mallory in the middle of this key exchange, she can create her own two secret keys and exchange communications with Alice and Bob forwarding the messages so Alice and Bob are none the wiser.
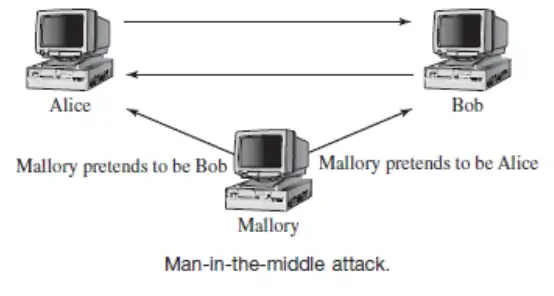
When Alice sends a message to Bob using what she thinks is the key Bob has, she really uses the one Mallory set up with her. The message is sent; Mallory intercepts it, decrypts it, reads or changes it, and then re-encrypts it with the key set up between Mallory and Bob.
Bob receives a message he believes to be from Alice when it is really from Mallory. Now Mallory has full control over the communication channel, and both confidentiality and integrity are lost because authentication was never established.
The Diffie-Hellman key exchange is still in use today; however, it is commonly used with authentication mechanisms to help mitigate man-in-the-middle attacks.
References and Credits
Wiley Pathways Network Security Fundamentals Project Manual, by Eric Cole, Ronald L. Krutz, James Conley, Brian Reisman, Mitch Ruebush, Dieter Gollman and Rachelle Reese.
»» You may also like this article: What is MCRA (Microsoft Cybersecurity Reference Architectures)?